根据数据存储逻辑以及使用场景主要分三类
一维数据结构
- 基础
- 数组 Array(String)
- 链表 Linked list
- 高级
- 栈 Stack
- 队列 Queue
- 双端队列 Deque
- 集合 Set
- 映射 Map (hash、map、dictionary)
二维数据结构
- 基础
- 高级
- 二叉搜索树 Binary search tree
- 红黑树 Red-black tree
- AVL 树 AVL
- 堆 Heap
- 并查集 Disjoint set
- 字典树 Trie
特殊数据结构
- 位运算 Bitwise
- 布隆过滤器 BloomFilter
- LRU Cache
算法基石
任何高级算法最终都会转换为以下几种逻辑处理
- if-esle、switch -> branch 跳转语句
- for、loop、while -> lteration 循环语句
- 递归 (Recursion) (Divide & Conquer,Bcktrace)
常见算法
- 搜索 Search ; 深度优先(Depth first search);广度优先(Breadth first search)
- 动态规划 (Dynamic Programming)
- 二分查找 (Binary Serach)
- 贪心 (Greedy)
- 数学 (Math),几何(Geomtry)
学习数据结构与算法必须步骤
- 每个算法至少要做5遍(非连续),第一遍5~10分钟读题,没有思路直接看解法,不要死磕!不要死磕!不要死磕!
- 第二遍12小时后,第三遍24小时后,第四遍一周后,第五遍面试前一周
- 每个算法尽可能多想几种解法,理解每个算法的执行逻辑、时间、空间复杂度
- PS : 编程时要养成对代码的时间、空间复杂度分析
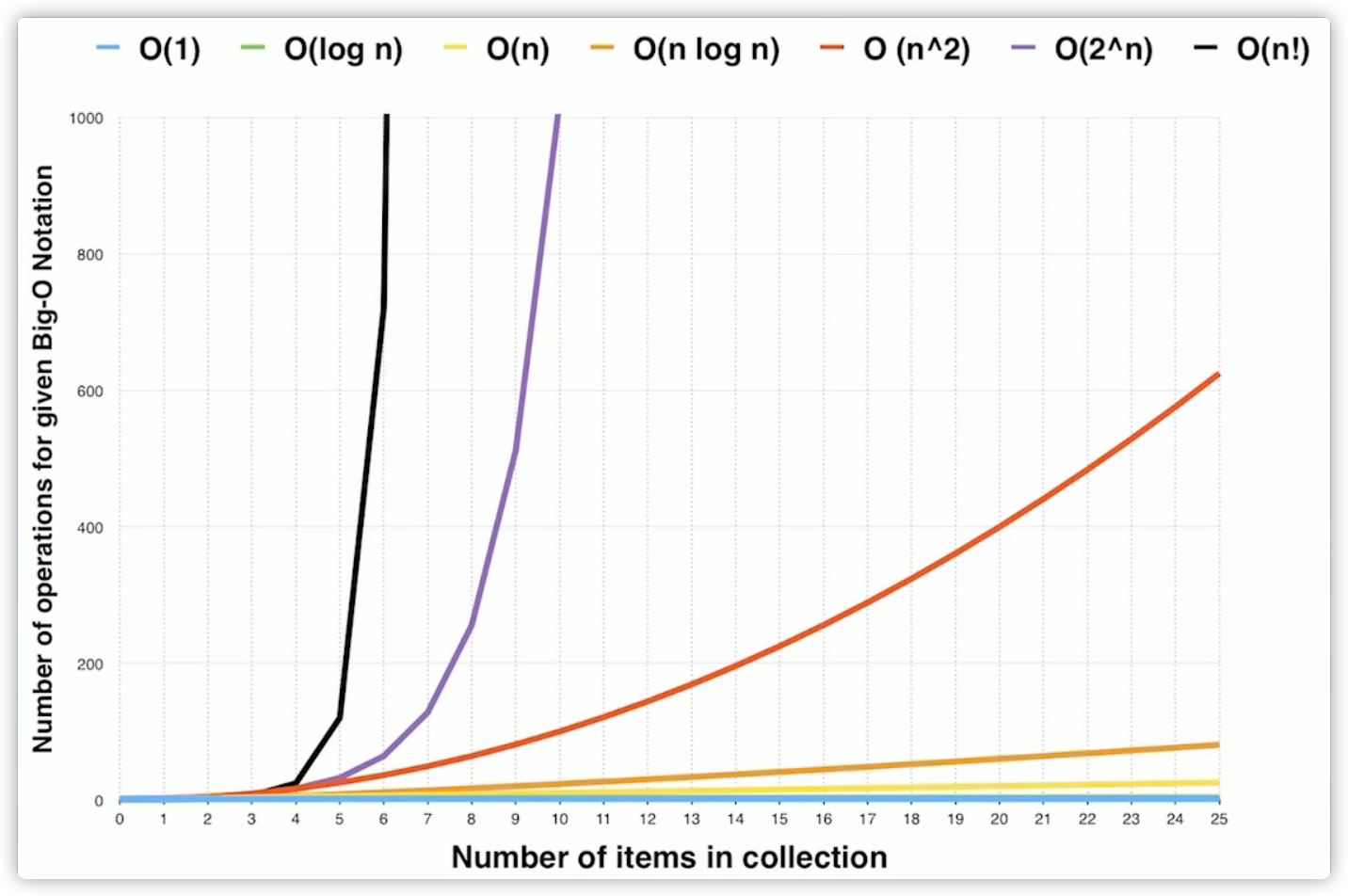
常见时间复杂度标志(以下顺序有低到高)[Big O notation]
- O(1) 常数时间复杂度(Constant Complexity )
- O(n) 线性时间复杂度(Liner Complexity)
- O(logn) 对数时间复杂度(Logarithmic Complexity)
- O(n^2) 平方时间复杂度(N Square Complexity)
- O(n^3) 立方时间复杂度(N Cube Complexity)
- O(2^n) 指数时间复杂度(Exponential Complexity)
- O(n!) 阶乘时间复杂度(Factorial)
理解时间复杂度分析方法
/*
例一:
代码执行两次输出,可以表示为 O(2),因为执行次数明确所以可以简化为O(1)
即使再增加N行,那么这个函数也依然是O(1) 常数时间复杂度
*/
void f1(){
System.out.println("1");
System.out.println("2");
}
/*
例二:
代码中有变量 n , 输出次数由 n 来控制,所以该函数的时间复杂度为 O(n) 线性时间复杂度
*/
void f2(){
int n=10000;
for(int i=0;i<n;i++){
System.out.println("1");
}
}
/*
例三:
代码中有变量 n 以及有两层循环,执行次数为外层次数乘以内层次数
表示为n*n,转换为大O既表示为 O(n^2),既平方级时间复杂度
*/
void f3(){
int n=10000;
for(int i=0;i<n;i++){
for(int j=0;j<n;j++){
System.out.println("1");
}
}
}
/*
例四:
代码中有变量 n 以及有两个循环,执行次数为第一个循环次数+第二个循环次数
表示为2*n,因为 2 是常数所以简化后表示为 O(n)
*/
void f4(){
int n=10000;
for(int i=0;i<n;i++){
System.out.println("1");
}
for(int j=0;j<n;j++){
System.out.println("1");
}
}
/*
例五:求斐波那锲数的第N项
递归时间复杂度分析
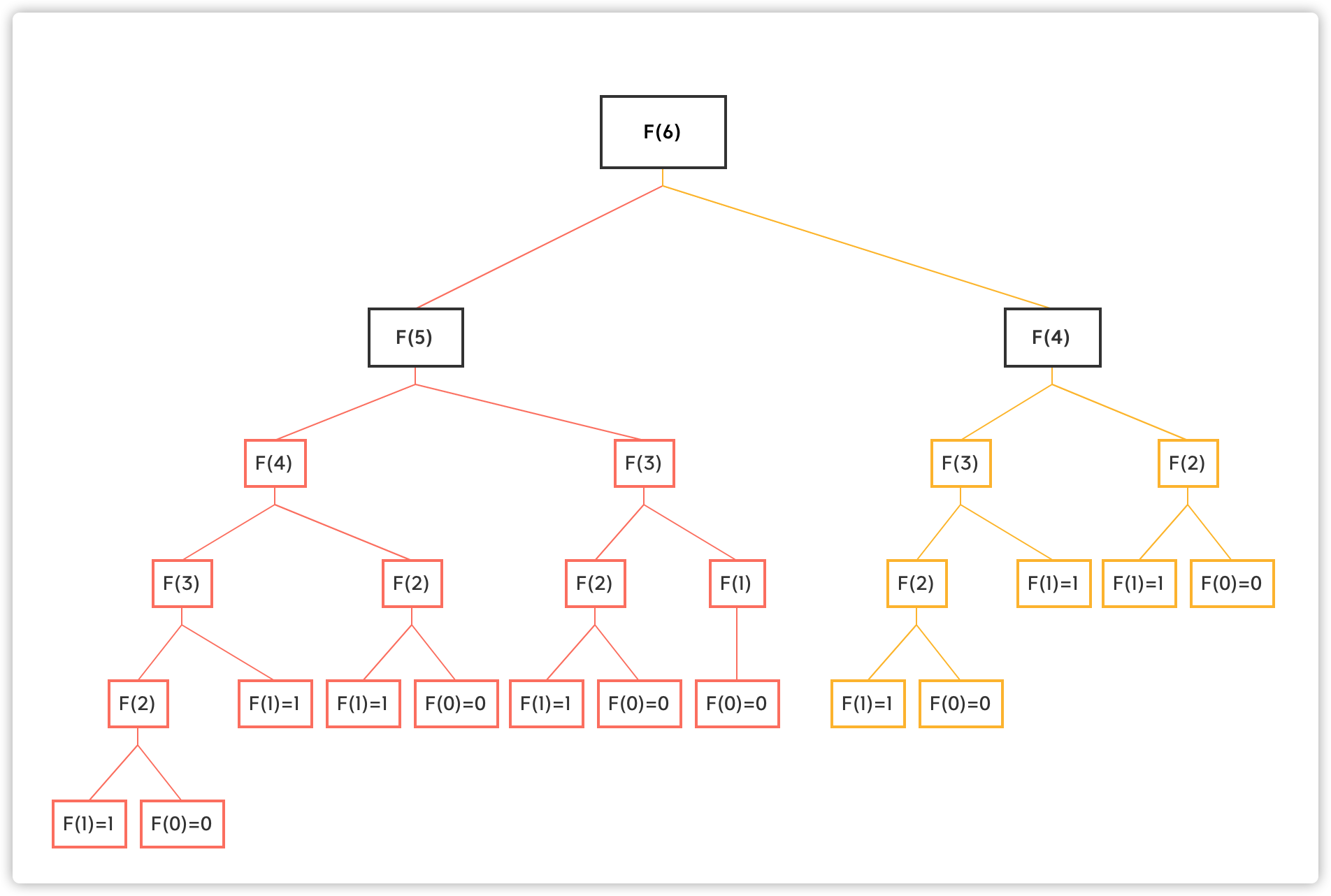
分析方法:将递归执行顺序画出一个树形结构,这个树形结构也可以称作状态树(参考后面的示意图)
根据示意图能看到两个现象
1、重复计算问题
2、由于大量重复计算(F(3\2\1)等等),最终算出来的时间复杂度为2^n(每次计算会展开两个节点所以是2^n)
PS:后面做ARTS时候会对 Fib 进行优化详解
*/
// Fib : 0,0,1,1,2,3,5,8,13,21
int fib(int n){
if(n<=2){
return n;
}
return fib(n-1)+fib(n-2);
}
- 递归状态树
- 时间复杂度曲线图
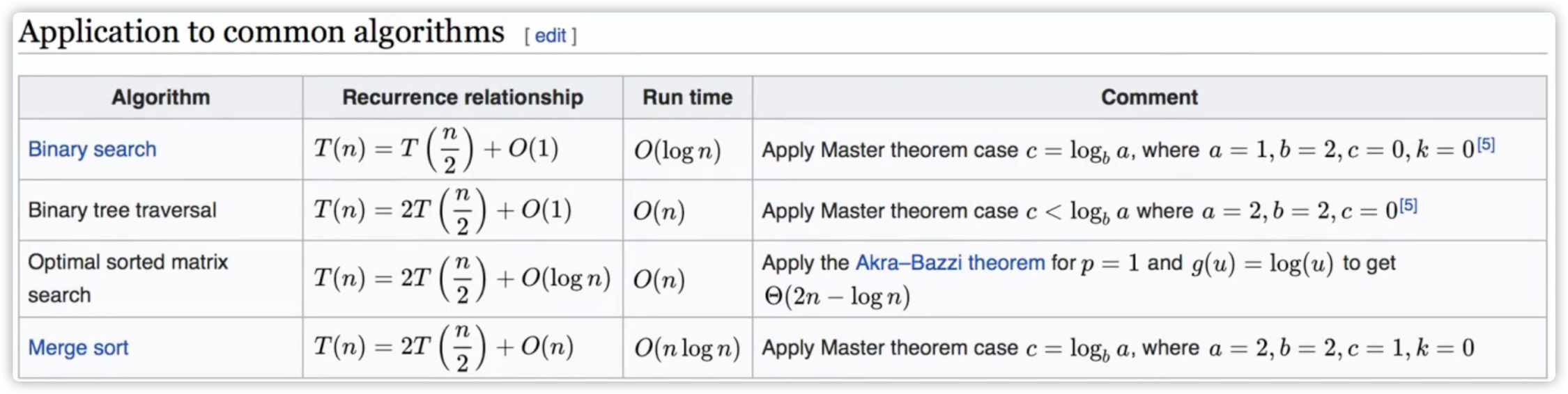
主定理 (Master Theorem)